Progression
A sequence of numbers is called a progression, where each succeeding number is related to the previous one by an arithmetic or geometric dependency.
Arithmetic Progression
An arithmetic progression is a series of numbers where each subsequent value is formed by adding the same number, the progression's common difference \(d\):
\(a_1 = a_{n-1} + d\);
Arithmetic progression belongs to monotonous sequences. When \(d > 0\), it increases; \(d < 0\), it decreases; \(d = 0\), it is stationary.
Example of an arithmetic progression: \(A = 1, 3, 5, 7, 9\). It is a monotonically increasing sequence of numbers with a common difference \(d = 2\).
Geometric Progression
A geometric progression is a series of numbers where each subsequent value is formed by multiplying it by the same number, the progression's common ratio \(q\):
\(b_n = b_1 \cdot q^{(n-1)}\);
Example of a geometric progression: \(B = 2, 4, 8, 16, 32, 64\). Its common ratio is 2.
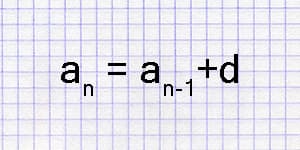
Our arithmetic progression calculator not only allows you to find the n-th term and the sum of its terms but also gives you fully described solving.
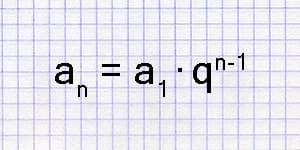
The geometric progression calculator enables you to ascertain the n-th term and the sum of its terms while also providing step-by-step solutions.