Arithmetic progression calculator
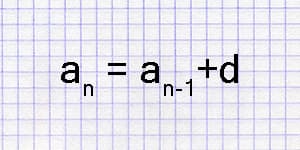
An arithmetic progression is a sequence of numbers in which the difference of any two consecutive members is a constant. This constant difference is known as the "common difference" and is denoted by the letter \(d\). The first term of the sequence is denoted as \(a_1\).
The general form of an arithmetic progression is expressed as: \[a_1, a_1 + d, a_1 + 2d, a_1 + 3d, \ldots\]
Here, \(a_1\) is the first term, and \(d\) is the common difference.
Key Characteristics
- Common Difference (\(d\)): As mentioned earlier, the common difference represents the fixed value by which each term in the sequence differs from the preceding one.
- N-th Term (\(a_n\)): The \(n\)-th term of an arithmetic progression is given by the formula: \[a_n = a_1 + (n - 1)d\]
- Sum of \(n\) Terms (\(S_n\)): The sum of the first \(n\) terms of an arithmetic progression can be calculated using the formula: \[S_n = \frac{n}{2} [2a_1 + (n - 1)d]\]
Example
Let's consider an arithmetic progression: 3, 7, 11, 15, 19. Here, \(a_1 = 3\) and \(d = 4\).
- The \(4\)-th term (\(a_4\)) can be found using the formula: \[a_4 = a_1 + (4 - 1)d = 3 + 3 \cdot 4 = 15\]
- The sum of the first \(4\) terms (\(S_4\)) is calculated as: \[S_4 = \frac{4}{2} [2 \cdot 3 + (4 - 1) \cdot 4] = 40\]
Applications
Arithmetic progressions have widespread applications, including:
- Finance: Calculating the future value of investments over time.
- Computer Science: Addressing problems related to loops and iterations.
- Physics: Modeling linear relationships and motion.
Conclusion
Understanding arithmetic progression is essential for tackling various mathematical and real-world problems. Whether you're dealing with financial calculations, writing computer programs, or analyzing physical phenomena, the principles of arithmetic progression provide a valuable foundation.
Comments on the calculator
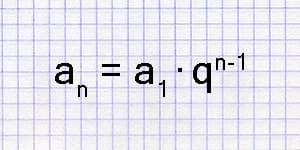
The geometric progression calculator enables you to ascertain the n-th term and the sum of its terms while also providing step-by-step solutions.
Go to calculation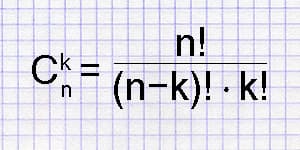
The combinations calculator helps you determine the count of potential combinations from a specified number of objects, denoted as "n choose k."
Go to calculation
The service will help factorize any composite number into its prime factors with a step-by-step solution.
Go to calculation