Geometric progression calculator
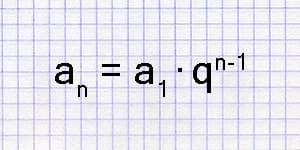
Geometric progression, often abbreviated as GP, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. This mathematical concept plays a crucial role in various fields and applications.
Structure of Geometric Progression
In a geometric progression, each term is calculated using the formula:
\[a_n = a_1 \cdot r^{(n-1)}\]
Where:
- \(a_n\) is the \(n\)-th term,
- \(a_1\) is the first term,
- \(r\) is the common ratio, and
- \(n\) is the number of terms.
The general form of a geometric progression looks like this:
\[a_1, a_1 \cdot r, a_1 \cdot r^2, a_1 \cdot r^3, \ldots\]
Key Properties of Geometric Progression
1. Common Ratio (\(r\)): The ratio between any two consecutive terms in a geometric progression is constant.
2. Exponential Growth or Decay: Depending on whether the common ratio is greater than 1 or between 0 and 1, a geometric progression exhibits exponential growth or decay, respectively.
Applications of Geometric Progression
Geometric progressions find applications in various areas:
- Finance: Compound interest calculations often involve geometric progressions.
- Physics: Concepts like exponential decay and growth are modeled using geometric progressions.
- Biology: Population growth and decay can be represented using geometric progressions.
- Computer Science: Algorithms and data structures may utilize geometric progressions.
Understanding geometric progression is essential for solving real-world problems and making informed decisions in diverse fields.
Comments on the calculator
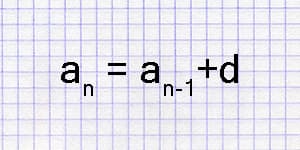
Our arithmetic progression calculator not only allows you to find the n-th term and the sum of its terms but also gives you fully described solving.
Go to calculation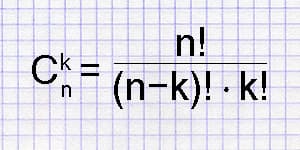
The combinations calculator helps you determine the count of potential combinations from a specified number of objects, denoted as "n choose k."
Go to calculation
The service will help factorize any composite number into its prime factors with a step-by-step solution.
Go to calculation