Volume of a truncated cone
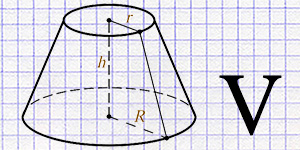
The truncated cone is one of the fundamental and important geometric figures in mathematics and physics. This figure is a cone with its top part cut off by a plane parallel to the base. The truncated cone is characterized by two circular bases of different diameters and a lateral surface formed by generators connecting corresponding points on these bases.
Historically, truncated cones have found widespread application in architecture and engineering. They are used in the structures of many architectural buildings, from ancient temples to modern buildings. Truncated cones are also used in various fields of engineering, such as in the design of turbines or ventilation systems.
Geometric Description of a Truncated Cone
A truncated cone is a three-dimensional geometric figure obtained by intersecting a regular cone with a plane parallel to its base. The geometric properties of the truncated cone include:
- Bases: two circular bases of different diameters, positioned parallel to each other.
- Lateral surface: an inclined surface formed by generators connecting the edges of the bases.
- Height (h): the perpendicular distance between the bases.
- Base radii (R and r): the radius of the larger and smaller bases, respectively.
- Generatrix (l): the distance from the edge of one base to the edge of the other, passing along the lateral surface.
Characteristics Table of a Truncated Cone:
| Characteristic | Description |
|---|---|
| Bases | Two parallel circles of different radii |
| Lateral Surface | Inclined, consists of generators |
| Height \( h \) | Perpendicular distance between the bases |
| Radii \( R \) and \( r \) | Radii of the larger and smaller bases, respectively |
| Generatrix \( l \) | Distance between the edges of the bases |
Mathematical Formula for Calculation
The mathematical formula for calculating the volume of a truncated cone is based on the areas of its bases and height. The volume formula \( V \) for a truncated cone is given as follows:
where:
- \( R \) and \( r \) are the radii of the larger and smaller bases of the truncated cone, respectively,
- \( h \) is the height of the truncated cone, measured as the perpendicular distance between the two bases.
This formula allows for precise determination of the volume of a truncated cone, knowing the sizes of its bases and height. It is important to note that the formula is applicable to both regular and irregular truncated cones, as it depends only on the dimensions of the bases and height.
The principle of calculation is based on the fact that the volume of a truncated cone is equal to the difference in volumes of two cones – a larger cone with a base radius \( R \) and height equal to the sum of \( h \) and the height of the smaller cone inscribed in the truncated cone, with radius \( r \).
Thus, understanding this formula and the ability to apply it in practice allows for accurate calculation of the volumes of truncated cones in various practical and theoretical tasks.
Practical Application
Knowledge of calculating the volume of a truncated cone is important in many fields, from engineering and architecture to education and science. Here are some of the most significant examples of practical use of this knowledge:
Engineering and Design. Truncated cones are often encountered in the design of various engineering structures and mechanisms. Calculating their volume helps in determining the weight and materials needed for their construction. Examples include elements of bridge structures or parts of machinery.
Architecture. In architecture, the truncated cone is used to create unique forms of buildings and structures. Knowledge of its volume helps architects in space planning and determining structural load.
Education and Science. In educational institutions, understanding how to calculate the volume of a truncated cone is an important part of geometry and mathematics courses. In scientific research, this knowledge is applied to study the physical properties of various materials and elements.
Industrial Production. In industry, calculating the volume of a truncated cone is necessary for designing various containers, pipes, ventilation systems, and other products.
Space Industry. In the aerospace industry, truncated cones are used in the designs of rockets and spacecraft. Precise calculations of their volumes are critically important for ensuring the correct fuel balance and flight stability.
Thus, knowing how to calculate the volume of a truncated cone opens up wide opportunities for its practical application in various industries, influencing the development of technology and scientific research.
Conclusion
The truncated cone is not just an abstract geometric figure, but also an object with wide application in the real world. From architecture to aerodynamics, from culinary arts to industrial design – understanding and being able to correctly calculate the volume of a truncated cone has tremendous practical significance. Knowledge of these principles allows us to more deeply understand and appreciate the multitude of objects and phenomena around us.
In this article, we have explored the key aspects of the truncated cone – from its geometric description to mathematical formulas for calculating volume. These insights not only broaden our understanding of geometry as a science but also provide practical tools for solving real-world problems in various fields of activity.
Comments on the calculator
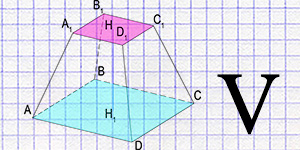
Calculation of the volume of a truncated pyramid through the values of the areas of the bases and height.
Go to calculation
Calculator for accurately calculating the volume of a cone using height or apothem and the base area or base radius.
Go to calculation
Calculator for accurately calculating the volume of a pyramid using the height and base area or one of the sides of the base.
Go to calculation