Cone volume
The cone is one of the fundamental geometric shapes that has found wide application in various fields of science, technology, and art. It is a solid of revolution formed by rotating a right-angled triangle around one of its sides. The cone is characterized by a circular base and a vertex that is located above the center of the base.
Historically, cones have been used in architecture, engineering, and even in religious symbols. From ancient times to modern days, they have served both practical and aesthetic purposes. In the architecture of ancient Egypt and Greece, conical shapes can be found in the design of buildings and monuments. In the modern world, the cone finds its application in aerodynamics, where its shape is used to create objects with minimal air resistance, such as rocket noses and airplane fuselages.
Geometric Description of the Cone
The cone is a geometric solid that consists of a circular base and a sloping surface converging at a single point, called the vertex. These basic elements define the shape and properties of the cone.
- Base: Circular in shape, positioned horizontally.
- Lateral Surface: Sloping, forming a circular sector.
- Vertex: The point located above the center of the base, where all lines of the lateral surface meet.
Table of Cone Characteristics:
| Characteristic | Description |
|---|---|
| Base | Circle |
| Vertex | Central point above the base |
| Height (h) | From vertex to base |
| Radius (r) | Distance from the center of the base to its edge |
| Generatrix (l) | From vertex to the edge of the base |
Formulas for the Cone:
- Height (h): The perpendicular distance from the vertex to the base.
- Radius (r): The distance from the center of the base to its edge.
- Generatrix (l): The distance from the vertex to the edge of the base, calculated using the Pythagorean theorem as \( l = \sqrt{h^2 + r^2} \).
Mathematical Formula for Calculating the Volume of a Cone
The volume of a cone is calculated based on its geometric characteristics – height and base radius. The formula for calculating the volume of a cone \( V \) is expressed as follows:
V = \(\frac{1}{3} \pi r^2 h\)
where:
- \( r \) – the radius of the base of the cone,
- \( h \) – the height of the cone, measured from the vertex to the center of the base.
This formula is based on the assumption that the base of the cone is a circle and the height is perpendicular to the base. It is important to note that the volume of a cone is one-third of the volume of a cylinder with the same base and height.
Application of the Formula
To calculate the volume of a cone, it is necessary to know its base radius and height. If the generatrix of the cone is known, the height can be calculated using the Pythagorean theorem:
h = \(\sqrt{l^2 - r^2}\)
where \( l \) is the generatrix of the cone. After determining all the necessary values, they can be substituted into the formula to calculate the volume.
Practical Application of Knowledge About the Volume of a Cone
Knowledge of how to calculate the volume of a cone has numerous practical applications in various fields. From industrial design to architecture, from geometry to applied mathematics, understanding the volume of a cone plays a key role in many areas. Below are some of the main examples of using this knowledge:
- Architecture and Construction: Conical structures are often used in architecture, for example, in domes and towers. Calculating their volume helps in planning materials and determining structural stability.
- Industrial Design: In mechanical engineering and design, cones may be used in parts of machines and mechanisms. Precise volume calculation is necessary to determine the capacity or weight of components.
- Education: In educational institutions, knowledge of calculating the volume of a cone is used to teach students the basics of geometry and mathematics.
- Science and Research: In the field of scientific research, the calculation of a cone's volume can be applied in physics and engineering, for example, when studying aerodynamic or hydrodynamic properties of objects.
- Culinary: In cooking, the cone shape is encountered in various types of packaging, such as ice cream cones. Calculating their volume helps to determine the necessary amount of ingredients.
Thus, understanding how to calculate the volume of a cone opens up many possibilities for its practical application in everyday life and professional activities.
Conclusion
The volume of a cone is an important geometric element, playing a key role in many areas, ranging from architecture to applied mathematics. Understanding how the volume of a cone is calculated promotes the development of mathematical thinking and finds wide application in real-world tasks. The accuracy of these calculations often determines the success of many engineering and design projects. Therefore, a deep understanding of the principles of calculating the volume of a cone is an integral part of education and professional activity in many fields.
References and Resources
- Kiselev A.P., "Elementary Mathematics. Geometry", Moscow: Enlightenment, 1987.
- MathWorld - Wolfram Web Resource, "Cone", available at [http://mathworld.wolfram.com/Cone.html]
- Khan Academy, "Geometry and Volume", available at [https://www.khanacademy.org/math/geometry]
These sources provide additional information about cones and their volumes, as well as about geometry in general, and can be useful for further exploration of the topic.
Comments on the calculator
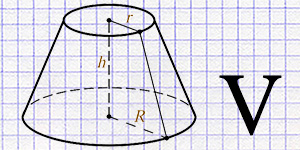
Calculation of the volume of a truncated cone using the radius of the lower and upper bases and height.
Go to calculation
Calculator for accurately calculating the volume of a pyramid using the height and base area or one of the sides of the base.
Go to calculation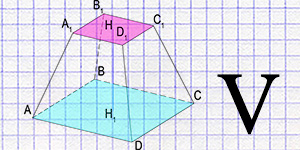
Calculation of the volume of a truncated pyramid through the values of the areas of the bases and height.
Go to calculation