Prism volume calculator

A prism is a polyhedron formed by two equal and parallel polygons called the bases of the prism, and rectangles or parallelograms that connect the corresponding sides of the bases, called lateral faces. Prisms are classified by the number of angles at the base and by the position of the lateral faces relative to the bases: a right prism has lateral faces perpendicular to the bases, while an oblique prism does not.
There are various types of prisms: regular, where the bases are regular polygons and the lateral edges are equal, and irregular, where the conditions of regularity are not met. A key parameter of the prism, along with surface area, is its volume - the amount of space bounded by its surfaces.
Geometric description of the prism
The prism is a three-dimensional figure in geometry that has interesting and important properties, making it applicable in various fields of science and engineering. To fully understand the prism, it is important to consider its geometric characteristics in more detail.
Main elements of the prism:
- Prism bases: Two parallel and equal polygons, located in different planes. The bases define the shape of the prism and can be any polygons, from triangles to polygons with a large number of sides.
- Lateral faces: Rectangles or parallelograms that connect the corresponding sides of the two bases. The number of lateral faces equals the number of sides of the polygon base.
- Edges: Segments that connect the corresponding vertices of the bases and are the sides of the lateral faces. The edges of the prism are divided into lateral edges and base edges.
- Vertices: Points at which the edges of the prism converge. The number of vertices in the prism is twice the number of vertices of the base.
Types of prisms:
- Right prism: Lateral edges are perpendicular to the bases, and the lateral faces are rectangles.
- Oblique prism: Lateral edges are inclined to the bases, and the lateral faces are parallelograms.
Features of the prism:
- A right prism with a regular polygon at the base is called a regular prism.
- The volume of the prism is defined as the product of the base area by the height of the prism (the distance between the bases).
Understanding these geometric features of the prism is key to studying its properties and applying it to solve problems.
Mathematical formula for calculating the volume of a prism
The main mathematical principle underlying the calculation of the volume of a prism is the multiplication of the area of the prism base by its height. This formula is universal and applicable to any type of prism, regardless of the shape of its base.
Prism Volume Formula:
\[ V = B \cdot h \]
where:
- \(V\) — the volume of the prism,
- \(B\) — the base area of the prism,
- \(h\) — the height of the prism, i.e., the perpendicular distance between the bases.
Application of the formula:
- For a right prism with a triangular base, where the base area (\(B\)) can be found as \(\frac{1}{2} \cdot base \cdot height\) of the triangle, and the height of the prism (\(h\)) equals the distance between the bases.
- In the case of a right prism with a rectangular base, \(B\) is calculated as the product of the length and width of the base.
- For an oblique prism, the formula remains the same, but it is important to correctly define the height, which is still measured as the perpendicular distance between the base planes.
Examples of calculation:
- If the base of a right prism is a square with a side of 4 m, and the height of the prism is 10 m, then the volume is calculated as \( V = 4^2 \cdot 10 = 160 \) cubic meters.
- For a right prism with a triangular base, where the base of the triangle is 3 m, the height of the triangle is 4 m, and the height of the prism is 6 m, the volume will be \( V = \frac{1}{2} \cdot 3 \cdot 4 \cdot 6 = 36 \) cubic meters.
This formula allows for quick and accurate determination of the volume of the prism, which is necessary in many tasks in geometry, physics, and engineering.
Methods for Finding the Volume of a Prism
The methods for finding the volume of a prism depend on the type of prism and the available initial data. The basic volume formula \(V = B \cdot h\), where \(B\) is the base area, and \(h\) is the height of the prism, can be adapted for different situations:
- Direct prism with a polygon at the base: For a direct prism with a polygon at the base, the volume is found by calculating the base area \(B\) as the sum of the areas of triangles or other figures into which the polygon can be divided, and multiplying it by the height \(h\).
\[V = B \cdot h\]
- Oblique prism: For an oblique prism, the volume is found in the same way as for a direct one, since the height \(h\) is measured perpendicularly to the bases, and the base area \(B\) remains the same.
- Using integral calculus: In cases where the prism has a variable base area along the height, the volume can be found using integral calculus, integrating the cross-sectional area along the height of the prism.
\[V = \int_{a}^{b} A(x) dx\]where \(A(x)\) is the cross-sectional area at height \(x\).
- Through diagonals and angles between them at the base: If the base of the prism is a polygon, and the diagonals and angles between them are known, the base area can first be found using the cosine theorem, and then multiplied by the height.
- Regular triangular prism: The volume is found using the formula \(V = \frac{\sqrt{3}}{4} a^2 h\), where \(a\) is the edge length of the base, and \(h\) is the height of the prism.
- Regular quadrilateral prism (cuboid): The volume is found using the formula \(V = a^2 h\), where \(a\) is the edge length of the base.
- Regular pentagonal prism: The volume is found using the formula \(V = \frac{5}{4} a^2 h \tan(\frac{\pi}{5})\), where \(a\) is the edge length of the base.
- Regular hexagonal prism: The volume is found using the formula \(V = \frac{3\sqrt{3}}{2} a^2 h\), where \(a\) is the edge length of the base.
These methods allow for the adaptation of prism volume calculations based on its type and available measurements, ensuring accuracy and versatility in solving geometric problems.
Practical Applications
Architecture and Construction: Knowing the volume of a prism is important in the design and construction of various architectural structures, such as buildings, bridges, and tunnels. It enables engineers to determine the necessary amount of building and finishing materials, as well as to estimate the overall cost of the project.
Manufacturing: In industry, knowledge of prism volume calculation is applied to determine the volume of containers, tanks, and other storage units. This optimizes the production process, inventory management, and logistics.
Education: In the educational process, learning methods to calculate the volume of a prism aids in developing spatial thinking in students, improving their analytical skills, and understanding geometric principles.
Science: In scientific research, especially in physics and chemistry, calculating the volume of a prism is necessary for experimental work, such as studying the properties of gases or liquids in enclosed containers.
Medicine: In the medical industry, particularly in pharmacology, knowledge of volume is used in designing packaging for medications, as well as in creating models for implantation.
Conclusion
Knowledge of calculating the volume of a prism has important practical significance in many areas of human activity. From education and science to engineering, construction, and medicine — understanding how to find the volume of a prism contributes to solving a wide range of tasks. This skill not only aids in specific professional tasks but also in the development of analytical thinking and spatial perception, making it indispensable in the modern educational and professional context.
Comments on the calculator

Calculator for accurately calculating the volume of a pyramid using the height and base area or one of the sides of the base.
Go to calculation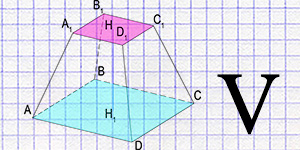
Calculation of the volume of a truncated pyramid through the values of the areas of the bases and height.
Go to calculation
Calculator for accurately calculating the volume of a cone using height or apothem and the base area or base radius.
Go to calculation