Permutations Calculator nPr
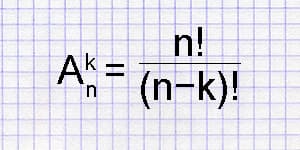
Permutations are an essential concept in combinatorics and probability theory, describing the arrangements of elements in a specific order. Whether you're solving mathematical problems, working with probability, or exploring algorithms, understanding permutations is crucial.
What Are Permutations?
A permutation is an ordered arrangement of distinct elements. The order of elements matters, meaning that changing the order results in a different permutation. For a set of \(n\) distinct elements, the number of permutations is denoted by \(n!\), read as "n factorial."
The factorial function is defined as the product of all positive integers up to a given number. Mathematically, it is expressed as:
\[ n! = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 1 \]Calculating Permutations
There are different scenarios in which permutations are calculated, depending on the constraints and requirements of the problem. Here are a few common cases:
Permutations without Repetition
When arranging \(r\) elements from a set of \(n\) distinct elements without repetition, the number of permutations is given by:
\[ P(n, r) = \frac{n!}{(n-r)!} \]Permutations with Repetition
When some elements are repeated in the set, the formula for permutations with repetition is:
\[ P(n; n_1, n_2, \ldots, n_k) = \frac{n!}{n_1! \cdot n_2! \cdot \ldots \cdot n_k!} \]where \(n_1, n_2, \ldots, n_k\) are the counts of each distinct element.
Applications of Permutations
Understanding permutations has various real-world applications. Some notable examples include:
- Cryptography: Permutations play a crucial role in creating secure encryption algorithms.
- Probability: Calculating permutations is essential in determining possible outcomes in probability experiments.
- Algorithm Design: Permutations are fundamental in designing algorithms for searching, sorting, and optimization.
- Game Theory: Permutations are used to analyze and strategize in games and decision-making scenarios.
Permutations are a fundamental concept with wide-ranging applications in mathematics and beyond. Whether you're exploring the elegance of combinatorics or tackling real-world problems, a solid understanding of permutations is a valuable asset. As you delve deeper into the world of permutations, you'll uncover their beauty and versatility in solving diverse problems.
Comments on the calculator
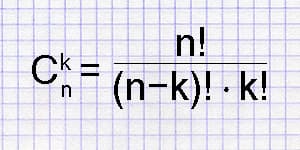
The combinations calculator helps you determine the count of potential combinations from a specified number of objects, denoted as "n choose k."
Go to calculation
The service will help factorize any composite number into its prime factors with a step-by-step solution.
Go to calculation
A Bernoulli trial is a random experiment with two possible outcomes, typically labeled as "success" and "failure".
Go to calculation