Bernoulli Trial Calculator

The Bernoulli trial is a fundamental concept in probability theory, named after the Swiss mathematician Jacob Bernoulli. It represents a random experiment with two possible outcomes, often referred to as "success" and "failure."
The Basics
In a Bernoulli trial, there are only two possible outcomes, and each trial is independent of the others. Let's denote:
- n: The number of trials.
- k: The number of successes.
- p: The probability of success in a single trial (ranging from 0 to 1).
The Formula
The probability mass function (PMF) for a Bernoulli distribution is given by the formula:
Where:
- P(X=k): Probability of having k successes.
- C(n, k): Combinations, denoting the number of ways to choose k successes from n trials.
The Bernoulli Theorem
The Bernoulli theorem describes the behavior of the sum of independent and identically distributed Bernoulli random variables. If X1, X2, ..., Xn are independent Bernoulli random variables with the same probability of success (p), then the sum Y = X1 + X2 + ... + Xn follows a binomial distribution.
Applications
Bernoulli trials find applications in various fields, including statistics, biology, and quality control. They are the foundation of the binomial distribution, which is widely used in modeling random phenomena.
Understanding the Bernoulli trial is crucial for grasping more complex probability concepts. Whether you're exploring the basics of statistics or diving into the intricacies of probability theory, the Bernoulli trial serves as a cornerstone in your mathematical journey.
Comments on the calculator
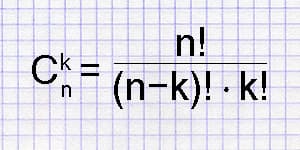
The combinations calculator helps you determine the count of potential combinations from a specified number of objects, denoted as "n choose k."
Go to calculation
The service will help factorize any composite number into its prime factors with a step-by-step solution.
Go to calculation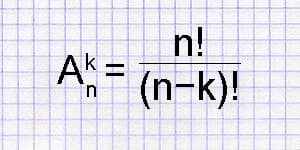
The permutations calculator calculates the number of possible arrangements of a given number of objects n taken k at a time.
Go to calculation